playmath

a boy’s math playground.

Cody Luo(cody@ustc.edu)

Records:

:star: 2010-02-04, I discovered Prime-Gap-Inequality: The i-th prime gap p[i+1]-p[i]<=i In other words, next_prime(n)-n <= primepi(n). This is because you can dispatch distinct prime factors for {p[i],p[i]+1,…,p[i+1]-1}.
Corollary: The i-th prime p[i]<=1+2+...+ i-1 + p[1] = i*(i-1)/2 +2.
:star: 2019-09-02, I proved Goldbach’s Conjecture! stage12-try to prove Goldbach Conjecture.ipynb
Note: in Sagemath env to run the codes

Goldbach Conjecture Inequality: gold(n) < prime_pi(prime_pi(n)+n) gold(n): the min non-negative integer g makes that both n-g and n+g are primes
prime_pi(n): the count of primes in 1..n

gold(n) < prime_pi(n), while n>344
gold(n) < prime_pi(n)*4395/3449751 ≈ prime_pi(n)*0.0013, while n>6*10^7
gold(n)=o(prime_pi(n)) as n-->+oo
:star: 2019-10-28, I solved 3n+1 Problem!
https://a-boy.github.io/playmath/stage26-3n%2B1conjecture/proving-3n%2B1-conjecture.html

# Syracuse function g(n)
def g(n):
    while n%2==0 : n/=2
    n=3*n+1
    while n%2==0 : n/=2
    return n

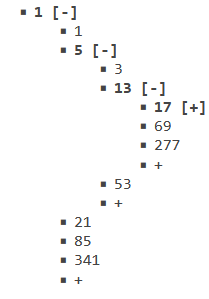part of Collatz Odd Tree Collatz-Odd-Tree1.png

Collatz-Odd-Tree Generating Rule

x is a leaf node in the full Collatz-Odd-Tree iff x%3==0
v(x)= x%3==1? (4*x-1)/3 : (2*x-1)/3 to generate the first child of x if x%3!=0
h(x)=4*x+1 to generate the next sibling of x. Because 3(4*x+1)+1 = 12*x+4 = 4*(3*x+1)

To prove 3n+1 Conjecture only needs to prove Collatz-Odd-Tree generating all positive odd integers. Obviously, starting from x0=1, h(x)=4*x+1 and v(x)=(2*x-1)/3 or (4*x-1)/3 will iterate all positive integers formed of 4k+1 or 4k-1, just all positive odd integers. Collatz Conjecture is proved!□

:star: 2018-03-06, I proved Twin Primes Conjecture and found a general law:

Prime-Gap-Subsegments-Theorem: In prime gap sequence, if any subsegment occurs twice, then it will continue to occur infinitely times. such as {2}, {4},{2*k},{2,4,2},{6,6},{2,6,4,2}...

stage9-Prime gap subsegment if repeats twice then infinitely times.nb

:star: 2023-09-09 I submitted a new sequence Historical Prime Factor hpf(n) to OEIS. Visit https://oeis.org/draft/A365521 for the latest revision of A365521 in OEIS.
:star: I discovered Bread Curve and Bread Model by chance in 2011:

def r(theta):= nest(sin,theta,1000)
polar_plot(r(theta),(theta,0,2*PI))

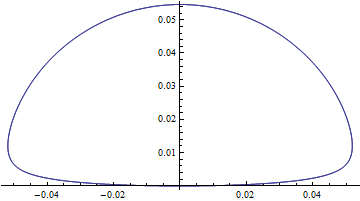
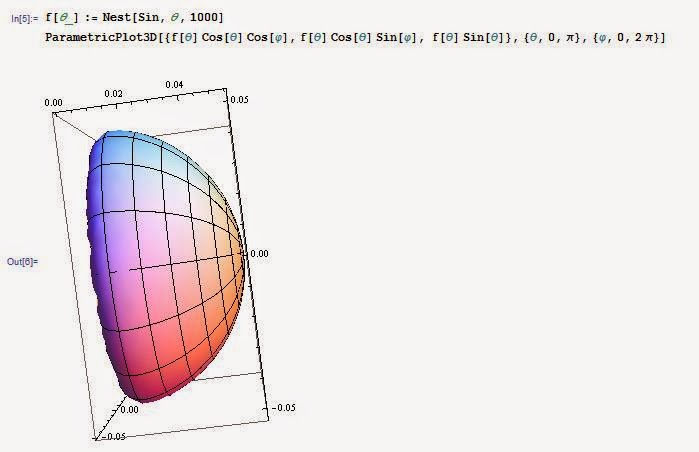
math and poem: 果中的泪滴.png
:star: 2022-02-07, I improved Oppermann’s Conjecture!

NextPrime-Of-Square-Inequality: next_prime(n^2) - n^2 <= 1+euler_phi(n)

:star: Ultra-Primes-Conjecture

Conjecture: There exists infinitely many primes formed of 2^(F[n!+1])-1 . here 2^p-1 is Mersenne number, F[n+2]=F[n+1]+F[n], 0,1,1,2,3,5,8,... is Fibonacci number, n! is factorial.

https://math.stackexchange.com/questions/3503947

2^F[2!+1]-1 = 3, 2^F[3!+1]-1= 2^13-1= 8191 are two known Ultra-Primes! I guess after 3, 8191 there are more prime heros!

:star: 2023-08-10,I proposed Plum Conjecture: when n>1 and 0<b<sqrt(n)-1, 2^(n^2±b)-1 is always composite. This is to say, the index p of a Mersenne prime 2^p-1 is NOT too close to some perfect square number.
:star: 2023-09-02, I formulated Fence-Conjecture:RamseyNumber(k+1,v+1)-1≡0,k,k+1mod(2k+1) , for k>1 and v>=k. The s(k,v) vertices of the critical Ramsey Graph can be laid out in k or k+1 staggered ways.

2023-11-22, I thinked that:

Ramsey Number R(m,n)=(2m-1)*p(2m-6+n,m)+{1,m,m+1}, for 3<=m<=n.

Here p(n,k) denote both the number of partitions of n into exactly k parts (that is, sums of k positive integers that add to n), and the number of partitions of n into parts of maximum size exactly k. see https://en.wikipedia.org/wiki/Triangle_of_partition_numbers .

Here denote S(k,l):=RamseyNumber(k+1,l+1)-1 . When constructing critical Ramsey graph for RamseyNumber(3,l+1)-1, I guess that the S(2,l) vertices can be laid out interlacing with 2 vertices and 3 vertices. This means S(2,v)%5 ∈{0,2,3}. R(3,n)≡1,3,4 mod 5 . (2010-?-?)

  o o o o o o o
    o   o   o  
  o o o o o o o

This conjecture implies R(3,10)=41, R(5,5)=46, and R(6,6)>=105.

idea:(mailto:cody@ustc.edu)

Goldbach-Triangle: every entry is the average of top and right primes. see https://oeis.org/A065305


3
4	5
5	6	7
7	8	9	11
8	9	10	12	13
10	11	12	14	15	17
11	12	13	15	16	18	19
13	14	15	17	18	20	21	23
16	17	18	20	21	23	24	26	29
17	18	19	21	22	24	25	27	30	31
20	21	22	24	25	27	28	30	33	34	37

I am a Goldbach triangle observer

Observation Conclusion 1: Using the first n-1 odd prime numbers { 3,5, … ,p[n]}, take half of the sum of any pair, and the result set will cover all integers between 3..(p[n]+p[n -prime_pi(n)])/2,without omissions…

n>=3, let p=nextprime(n!)-n! , then p is always prime or 1, because p is less than ` nextprime(n)^2 , very often p<n^2 `
Guess: for any ineteger n>=1, RamseyNumber(n+1,n+1)-1 = S(n,n) contains only the factors of Fermat Numbers ` F[m]=2^2^m+1 `, {1,2,3,5,17,257,641,65537,…} S(2,2)=5, S(3,3)=17, I guess S(4,4)=45
try to prove Twin Prime Conjecture

    1. Method 1: If a prime gap subsegment repeats twice, then it will occur infinitely times. 
    such as {2}, {4},{2*k},{2,4,2},{6,6}...
    1. Method 2: by using modern database function `groupby` on prime gap sequence, ...  
     Observing prime gap frequency distribution for primes up to some big integer N0 .  
     Peaks occur at multiples of 6. And the ratio of {2}s to {6}s will be great than a const(0.5 ?).
    1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14, 4, 6, 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, 4, 2, 12, 12, 4, 2, 4, 6, 2, 10, 6, 6, 6, 2, 6, 4, 2, ... (sequence A001223 in the OEIS).

define the integer sequence x[n+1]:=x[n]^2+1, if take x[0]>1, then x[5] is very often composite.
定义:二密分解 n=q1*q2 , q1取小于或等于√n的最大因数, q2取大于或等于√n的最小因数。是否值得尝试，使用二密分解或p-密分解的一些性质证明费马大定理?
Odd Primes Mask, if is_prime(2*k+1) 1 else 0

opm=OddPrimesMask=
011101101101001100101101001001100101100101001000101101101000000101
 357                                                         (127)

可能将圆周率Pi的二进制值分段，形成一个有规律的数组吗？如果可以的话，计算Pi的值就存在与之对应的极速算法。

  1   2   4    135     60753
  1|1.0|0100|10000111|1110110101010001|00010000101101000110000100011010011000100110001100110001010001011100000001101110000011100110100010010100100000010010011100000100010001010011001111100110001110100000000100000101110111110101001100011101100010011100110110010001001

Question

Inertia Law and Polar Method for integer sequences. 整数数列的惯性定理和极性定理

math tools

Mathematica : .nb is Mathematica notebook
Sagemath : .ipynb is Jupyter notebook, most of *.ipynb files in a-boy/playmath are used Sagemath, to view by Jupyter nbviewer, but to run codes only in Sagemath env; .sagews is Sagemath worksheet
Maple
GeoGebra
Octave
PARI/GP
MathType
Manim

赞助支持

PayPal: https://paypal.me/luojl

BTC: bc1qtlkhl9cusez69pephgfljuqzy5nht3la4r7vy0

感谢你的赞助和支持，希望我们每天都能做得更好！！！


3
4	5
5	6	7
7	8	9	11
8	9	10	12	13
10	11	12	14	15	17
11	12	13	15	16	18	19
13	14	15	17	18	20	21	23
16	17	18	20	21	23	24	26	29
17	18	19	21	22	24	25	27	30	31
20	21	22	24	25	27	28	30	33	34	37


3
4	5
5	6	7
7	8	9	11
8	9	10	12	13
10	11	12	14	15	17
11	12	13	15	16	18	19
13	14	15	17	18	20	21	23
16	17	18	20	21	23	24	26	29
17	18	19	21	22	24	25	27	30	31
20	21	22	24	25	27	28	30	33	34	37


3
4	5
5	6	7
7	8	9	11
8	9	10	12	13
10	11	12	14	15	17
11	12	13	15	16	18	19
13	14	15	17	18	20	21	23
16	17	18	20	21	23	24	26	29
17	18	19	21	22	24	25	27	30	31
20	21	22	24	25	27	28	30	33	34	37